Archiv für 2013-5

Kurztipp: DVD-Wiedergabe unter Lubuntu

Frage: „omfgomfg Dein dummes Nicht-Windows kann ja nicht mal DVDs abspielen!!11einself“

Antwort: Installiere lubuntu-restricted-extras und libdvdread4. Führe (als root) /usr/share/doc/libdvdread4/install-css.sh aus. Etwa so:

sudo apt-get install lubuntu-restricted-extras libdvdread4
sudo /usr/share/doc/libdvdread4/install-css.sh

Kurztipp: Dateien serverlos im Heimnetz verschicken

Häufig möchte ich eine Datei oder einen Link von einem Gerät auf ein anderen im Heimnetz schicken. Gero hatte vorgeschlagen, die Chrome-Tabs von einem Gerät auf ein anderes zu schicken. Das ist prinzipiell eine recht hübsche Angelegenheit. Diese Möglichkeit setzt jedoch voraus, dass der eigene Chromium-Browser über den Google-Account synchronisiert ist. Außerdem beschränkt sich dieser nette Trick auf den Austausch von Links zu vorhandenen Dokumenten. Wer jedoch private Dateien durch das Heimnetz schicken möchte, kann dies (fast) mit den Bordmitteln einer aktuellen Linuxdistribution tun: Die jede ist vom zerconf/avahi-Chat.

Zunächst sollte Avahi mDNS/DNS-SD daemon installiert sein. Dadurch „finden“ sich die Computer bzw. die darauf laufenden Dienste serverlos im lokalen Netzwerk. Nun fehlt noch ein geeigneter Chat-Client. Unter vielen Linuxdistributionen ist oft sind oft die Chatprogramme Empathy oder Pidgin installiert. Auch der reine XMPP-Client Gajim kann verwendet werden.

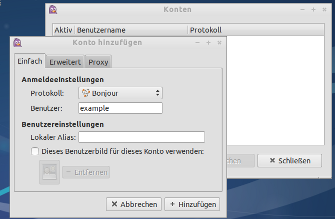
Ich habe mich für Pidgin entschieden. Dort musste ich einfach ein neues Chatkonto für das Protokoll „Bonjour“ einrichten. Ich musste mir lediglich einen Namen aussuchen und „Speichern“ klicken. Das ist alles. Unter Empathy hätte ich ein „Personen in der Nähe“-Konto eingerichtet und unter Gajim hätte ich das vorhandene „local“-Konto aktiviert.

Ist das Konto eingerichtet, tauchen die anderen Nutzer im Netzwerk automatisch in der Kontaktliste auf - ganz ohne Registrieren, Anmelden und „Kontakte hinzufügen“. Nun können einfach Dateien oder Textnachrichten wie etwa Links versendet werden.

Popcorn mal anders

Gerade jetzt zur Zeit der Jahrmärkte und Dorffeste treibt eine widerlich-klebrige von Mainstreamkinos bekannte, als Wurfgeschoss missbrauchte Masse ihr Unwesen in Deutschland. Die Rede ist vom so genanten Popcorn. Dem guten Puffmais wird jedoch bei dieser Verallgemeinerung Unrecht getan. Denn dieser existiert jedoch nicht nur in seiner widerlich-klebrigen gezuckerten Variante. Dies scheint offenbar nur eine deutsche Zubereitungsart zu sein. Etwa in den USA ist diese gezuckerte Version eher unbekannt. Dort ist höchstens gelegentlich „Kettle Corn“ vorzufinden. Dieses Knabberwerk wird zwar auch mit Zucker und Öl hergestellt, enthält jedoch dennoch Salz. Somit unterscheidet es sich vom deutschen Zuckerpopcorn, das ja gar nicht salzig ist. Übrigens ist salziges Popcorn in den vereinigten Staaten gar nicht unüblich. Es ist sogar die Regel! Amerikanisches Popcorn ist meist salzig. Das Salz wird meist nach der Zubereitung zugegebn.

Die Variantenvielfalt bei Popcorn ist nicht auf Zucker und Salz beschränkt. Eine eher untypische Variante ist das fein-würzige Popcorn. Es ist zuckerfrei und hat einen leichten Chiligeschmack. Diese Popcornart ist nicht nicht unebdingt jedermanns Geschmack. Es lohnt sich jedoch dies ein mal zu probieren – nicht nur als Testlauf für hausgemachtes Chiliöl.

Hausgemachtes Chiliöl

Eine wichtige Zutat beim würzigen Popcorn ist das Chiliöl. Dieses verleiht Popcorn und vielen anderen Speisen einen leicht-würzigen Geschmack. Chiliöl gibt es im gut sortierten Supermarkt zu kaufen. Allerdings lässt es sich deutlich preiswerter aus handelüblichem Speiseöl und Chiliflocken, also zerkleinerten, getrockneten Chilischoten herstellen.

Zur Herstellung benötigt werden Chiliflocken, Öl, eine Flasche und ein Trichter. Als Öl ist ein natives Olivenöl oder „Natives Olivenöl Extra“ zu empfehlen. Ideal, aber eher selten ist kaltgepresstes Maisöl. Eher abzuraten ist von Sonnenblumenöl.

Zunächst wird eine zwei Finger breite Schicht Chiliflocken mithilfe des Trichters in die Flasche gefüllt. Anschließen wird das Öl dazugegeben. Nun muss die Flasche kräftig durchgeschüttelt werden. Anschließend wird die Flasche in den Kühlschrank gestellt. Die Flocken quellen auf. Das Öl wird dickflüssig. Alle zwei bis drei Tage muss das Öl aus dem Kühlschrank genommen werden. Wenn es warm wird, setzen sich die Flocken langsam auf dem Boden ab. Nun wird das Öl wieder ein mal kräftig durchgeschüttelt und für die nächsten zwei bis drei Tage in den Kühlschrank gestellt.

Mit der Zeit nimmt das Öl eine gesunde rote Farbe an. Nach zwei Wochen kann es dann verwendet werden. Dazu kann das Öl durch ein Sieb umgefüllt werden, um keine Flocken mehr im Endprodukt zu haben. Es ist jedoch auch möglich die Flocken im Öl zu belassen. Bei vorsichtigem Ausgießen gelangen dann auch keine oder kaum Flocken in das Nahrungsmittel.

Würziges Popcorn mit leichtem Chiligeschmack

Das so hergestellte Chiliöl kann nun verwendet werden, um würziges Popcorn herzustellen. Neben dem Öl werden hierzu Puffmais (auch bekannt als Popcornmais, erhältlich im Supermarkt) und eine Pfanne mit durchsichtigem Deckel benötigt. Ist keine Pfanne verfügbar, kann auch ein Topf verwendet werden. Auf den Deckel sollte jedoch auf gar keinen Fall verzichtet werden!!1! (Es sei denn, dies geschieht für eine Fernsehsendung von Wigald Boning und Bernhard Hoëcker)

Zunächst muss die Oberfläche der Pfanne mit etwas Chiliöl benetzt werden. Gerade so viel, dass es reicht, um die Pfanne dünn damit zu bedecken. Es ist darauf zu achten, dass keine Chiliflocken in der Pfanne sind! Diese verbrennen nämlich und hinterlassen einen stechenden, die Schleimhäute reizenden Geruch. Das muss nicht sein. Nun muss das Öl so lange erwärmt werden, bis ein klein wenig Rauch aufsteigt. Dann sollte die Wärme etwas reduziert werden.

Danach werden die Maiskörner zugegeben. Hierbei sind so viele Maiskörner zu verwenden, dass die Hälfte der Pfanne mit einer Schicht der Körner bedeckt ist. Ist die Hälfte bedeckt, wird der Deckel aufgesetzt und die Maiskörner werden durch Rütteln über die ganze Pfanne verteilt.

Sobald die Körner zu knallen anfangen, muss die Pfanne gelegentlich gerütttelt werden. Sobald es nach intensivem Knallen keine entsprechenden Kanllgeräusche mehr gibt, muss die Pfanne von der Feuerstelle genommen werden.

Das deduktive System F0

Das deduktive System F₀ ist ein Kalkül. Es erlaubt durch eine reine Betrachtung des „wörtlichen“ (syntaktischen) Aufbaus einer Aussage Folgerungen zu treffen. Dies beutet außerdem, dass automatisiert Beweise für Aussagen gefunden werden können.

Wie jeder Kalkül gibt auch F₀ eine Menge von Axiomen (eigentlich: Axiomschemata) und Regeln vor. F₀ verwendet „Modus Ponens“ als einzige Regel. „Modus Ponens“ besagt, dass die rechte Seite einer Implikation bewiesen ist, wenn schon die Implikation selbst und die linke Seite bewiesen wurden. Gibt es also einen Beweis für A → B und A, so kann auch B als bewiesen angenommen werden. Die Axionsschemata in F₀ sind drei Formen Tautolgien, die nur die Negation (¬) und die Implikation (→) verwenden. Durch Einsetzen beliebiger Formlen (die nur → und ¬ verwenden) in diese Schemata, lassen sich bewiesene Aussagen generieren.

Neben den Axiomen gibt es außerdem noch eine Reihe von Theoremem, die schon bewiesen sind und wie die Axiomschemata verwendet werden dürfen. Auf der Webseite zur Logik im Sommersemester 2011 (Madlener) ist eine Zusammenfassung der Kalküle zu finden. Diese beinhaltet elf Theoreme und die drei Axiome aus F₀

Beispiel: z.Z. ⊢_F0 B → (¬C → ¬(B → C))

Wie wird ein Beweis in F₀ nun aufgeschrieben? Ich werde dies nun vorführen, indem ich Beweise, dass B → (¬C → ¬(B → C)) eine Tautologie ist. Die bedeutet, dass ich nur die Axiome (und nach Belieben die bewiesenen Theoreme) verwenden darf, um die Aussage herzuleiten. Es bietet sich an, das Deduktionstheorem anzuwenden:

• z.Z. ⊢_F0 B → (¬C → ¬(B → C))
• z.Z. B ⊢_F0 ¬C → ¬(B → C)

Es genügt also B als bewiesen anzunehmen und ¬C → ¬(B → C) herzuleiten.

1. B (als bewiesen angenommen)
2. ((B → C) → C) → (¬C → ¬(B → C)) (Theorem 8)
3. B → ((B → C) → C) (Theorem 5)
4. (B → C) → C (Modus Ponens 1. und 3.)
5. ¬C → ¬(B → C) (Modus Ponens 3. und 2.)

Das war es auch schon. Wichtig ist hierbei, immer die verwendeten Axiome (beziehungsweise Theoreme) und die mit Modus Ponens resultierenden Folgerungen getrennt voneinander auszuschreiben. Hier etwa hätte es nicht genügt 4. aufzuschreiben, ohne vorher 3. zu kennzeichnen!

Beispiel: z.Z. ⊢_F0 (A → B) → (¬B → ¬A)

Im vorigen Beispiel wurde das Theorem 8 verwendet. Als weiteres Beispiel werde ich dieses nun herleiten. Es erinnert stark an Axiom 3 ((¬A → ¬B) → (B → A)). Durch Einsetzen von ¬A und ¬B in Axiom 3 lässt sich auch etwa sehr Ähnliches bekommen: (¬¬A → ¬¬B) → (¬B → ¬A) In der semantischen Welt könnte einfach ¬¬A durch A und ¬¬B durch B ersetzt werden. Da in F₀ jedoch alles syntaktisch ist, geht das nicht. Es ist insbesondere auch nicht erlaubt die Negationen wegzulassen und „siehe Theorem 3 (¬¬A → A)“ zu schreiben. Sinnvoll ist hier ein Zwischenbeweis.

Zwischenbeweis: z.Z. ⊢_F0 (A → B) → (¬¬A → ¬¬B)

Zweifache Anwendung des Deduktionstheorems

• z.Z. ⊢_F0 (A → B) → (¬¬A → ¬¬B)
• z.Z. (A → B) ⊢_F0 ¬¬A → ¬¬B
• z.Z. (A → B), ¬¬A ⊢_F0 ¬¬B

(A → B) und ¬¬A werden also als gegeben angenommen und ¬¬B ist herzuleiten.

1. A → B (als bewiesen angenommen)
2. ¬¬A (als bewiesen angenommen)
3. ¬¬A → A (Theorem 3)
4. A (Modus Ponens 2. und 3.)
5. B (Modus Ponens 4. und 1.)
6. B → ¬¬B (Theorem 7)
7. ¬¬B (Modus Ponens 5. und 6.)

Anwendung des Zwischenbeweises

Der Zwischenbeweis ist nun ungemein hilfreich. Zunächst wird das Deduktionstheorem benutzt.

• ⊢_F0 (A → B) → (¬B → ¬A)
• (A → B) ⊢_F0 (¬B → ¬A)

Nun kann der Zwischenbeweis leicht eingesetzt werden:

1. A → B (als bewiesen angenommen)
2. (A → B) → (¬¬A → ¬¬B) (Aus dem Zwischenbeweis)
3. ¬¬A → ¬¬B (Modus Ponens 1. und 2.)
4. (¬¬A → ¬¬B) → (¬B → ¬A) (Axiom 3)
5. ¬B → ¬A (Modus Ponens 3. und 4.)

Weitere Beispiele finden sich in den Übungsaufgaben vom Sommersemester 2011.